3) Request the density of the Nth state of interest to be recovered from the checkpoint file with the following route section: # TD(Read,Root=N) LOT Density=Current Guess=Read Geom=AllCheck. Replace N for the Nth state which caught your eye in step number 2) and LOT for the Level of Theory you’ve been using in the previous steps.
- Read Checkpoint File Gaussian Software
- Read Checkpoint File Gaussian Free
- Read Checkpoint File Gaussian Pdf
- Read Checkpoint File Gaussian File
- If no file name is supplied in the input file, the checkpoint files are generated during program execution, but deleted on successful termination of the program. The line directly following these two lines is the first one absolutely necessary for the program to execute at all and contains keywords defining the major steps of the calculation to.
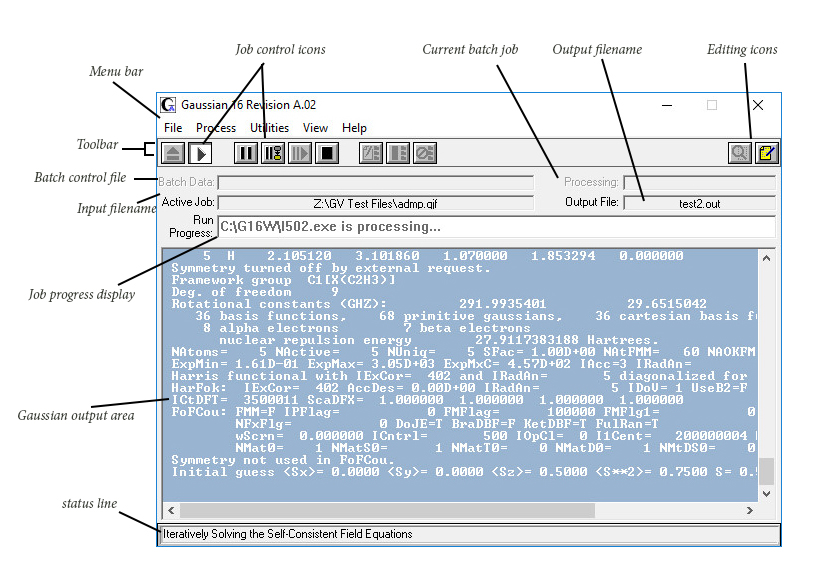
- Gaussian Tip: Finding out What’s in a Checkpoint File Ever wonder what’s in some of the numerous checkpoint files you have accumulated or which checkpoint file of several is the one you want? The chkchk utility will show you information about the job that created a checkpoint file.
- Functions for reading information from the checkpoint file. Each primitive Gaussian contributes to only one shell (and one basis function.
- Many such result are put in a file called a checkpoint file. It is a binary file. The use of a checkpoint file can be specified using the correct options on line 2 and the route card. Cube files: Properties, such as electron density or spin density can be calculated for a regular grid of points in space and saved as a cube file.
There are three molecular mechanics methods available in Gaussian. They were implemented for use in ONIOM calculations, but they are also available as independent methods. No basis set keyword should be specified with these keywords.
The following force fields are available:
AMBER: The AMBER force field as described in [37]. The actual parameters (parm96.dat) have been updated slightly since the publication of this paper. We use this current version from the AMBER web site (amber.scripps.edu).
DREIDING: The DREIDING force field as described in [38].
UFF: The UFF force field as described in [39].
CHARGE ASSIGNMENT-RELATED OPTIONS
Unless set in the molecule specification input, no charges are assigned to atoms by default when using any molecular mechanics force field. Options are available to estimate charges at the initial point using the QEq algorithm under control of the following options for any of the mechanics keywords:
QEq
Assign charges to all atoms using the QEq method [40].
UnTyped
Assign QEq charges only to those atoms for which the user did not specify a particular type in the input.
UnCharged
Assign QEq charges for all atoms which have charge zero (i.e., all atoms which were untyped or which were given a type but not a charge in the input).
PARAMETER PRECEDENCE OPTIONS
Terminology: Gaussian contains built-in parameter sets for the built-in force fields listed above; these are referred to as hard-wired parameters. Soft parameters are ones specified by the user in the input stream for the current job (or a previous job when reading parameters from the checkpoint file). By default, when no relevant option is given, the hard-wired parameters are the only ones used.
HardFirst
Read additional parameters from the input stream, with hard-wired parameters having priority over the read-in, soft ones. Hence, read-in parameters are used only if there is no corresponding hard-wired value. Note that wildcards matches within the hardwared parameter set take precidence over soft parameters, even when the latter contains an exact match for the same item. Use SoftFirst if you want to override hard-wired parameter matches.
SoftFirst
Read additional parameters from the input stream, with soft (read-in) parameters having priority over the hard-wired values.
SoftOnly
Read parameters from the input stream and use only them, ignoring hard-wired parameters.
ChkParameters
Read parameters from the checkpoint file. Any non-standard (soft) parameters present in the checkpoint file are used with higher priority than corresponding hard-wired parameters, unless HardFirst is also specified.
NewParameters
Ignore any parameters in the checkpoint file.
Modify
Read modifications and additions to the parameter set (after it has been constructed from hard and/or soft parameters).
HANDLING MULTIPLE PARAMETER SPECIFICATION MATCHES
Since parameters can be specified using wildcards, it is possible for more than one parameter specification to match a given structure. The default is to abort if there are any ambiguities in the force field. The following options specify other ways of dealing with multiple matches.
FirstEquiv If there are equivalent matches for a required parameter, use the first one found.
LastEquiv
If there are equivalent matches for a required parameter, use the last one found.
INPUT CONVENTIONS
AMBER calculations require that all atom types be explicitly specified using the usual notation within the normal molecule specification section:
Consult the AMBER paper [37] for definitions of atom types and their associated keywords.
Atom types and charges may also be provided for UFF and DREIDING calculations, but they are not required. For these methods, the program will attempt to determine atom types automatically.
Analytic energies, gradients, and frequencies.
ONIOM, Geom=Connect
GENERAL MOLECULAR MECHANICS FORCE FIELD SPECIFICATIONS
Unless otherwise indicated, distances are in Angstroms, angles are in degrees, energies are in Kcal/mol and charges are in atomic units. Function equivalencies to those found in standard force fields are indicated in parentheses. In equations, R refers to distances and θ refers to angles.
Wildcards may be used in any function definition. They are indicated by a 0 or an asterisk.
In MM force fields, the non-bonded (Vanderwaals and electrostatic) interactions are evaluated for every possible pair of atoms. However, interactions between pairs of atoms that are separated by three bonds or less are usually scaled down (in most force fields, using a factor 0.0 for pairs separated by one or two bonds, and some value between 0.0 and 1.0 for pairs that are separated by three bonds).
There are a number of ways to implement the calculation of non-bonded interactions. We follow a two-step procedure. First, we calculate the interactions between all pairs, without taking the scaling into account. In this step, we can use computationally efficient (linear scaling) algorithms. In the second step, we subtract out the contributions that should have been scaled, but were included in the first step. Since this involves only pairs that are close to each other based on the connectivity, the computer time for this step scales again linearly with the size of the system. Although at first sight it seems that too much work is done, the overall algorithm is the more efficient than the alternatives.
In the soft force field input, the NBDir function entry corresponds to the calculation of all the pairs, and the NBTerm entry is used for the subsequent subtraction of the individual pairs. However, to make things easier, you can specify just the non-bonded master function NonBon, which is automatically expanded into the actual functions NBDir and NBTerm during pre-processing.
Vanderwaals parameters, used for NBDir and NBTerm (See MMFF94 below for MMFF94-type Vanderwaals parameters).
VDWBond-length Well-depth
MMFF94 type Vanderwaals parameters (used for NBDir and NBTerm).
VDW94Atomic-pol NE Scale1 Scale2 DFlag
Atomic-pol Atomic polarizability (Angstrom3).
NE Slater-Kirkwood effective number of valence electrons (dimensionless).
Scale1 Scale factor (Angstrom1/4).
Scale2 Scale factor (dimensionless).
DFlag 1.0 for donor type atom, 2.0 for acceptor type, otherwise 0.0.
MMFF94 electrostatic buffering
Buf94Atom-type Value
Non-bonded interaction master function. This function will be expanded into pairs and a direct function (NBDir and NBTerm) before evaluation of the MM energy.
NonBonV-Type C-Type, V-Cutoff C-Cutoff VScale1 VScale2 VScale3 CScale1 CScale2 CScale3
V-Type is the Vanderwaals type:
0 No Vanderwaals
1 Arithmetic (as for Dreiding)
2 Geometric (as for UFF)
3 Arithmetic (as for Amber)
4 MMFF94-type Vanderwaals
C-Type is the Coulomb type:
0 No Coulomb
1 1/R
2 1/R2
3 1/R buffered (MMFF94)
V-Cutoff and C-Cutoff are the Vanderwaals and Coulomb cutoffs (respectively):
0 No cutoff
>0 Hard cutoff
<0 Soft cutoff
VScale1-3 are Vanderwaals scale factors for 1 to 3 bond separated pairs. CScale1-3 are Coulomb scale factors for 1 to 3 bond separated pairs. If any scale factor < 0.0, the 1/1.2 scaling is used (as for Amber).
Coulomb and Vanderwaals direct (evaluated for all atom pairs).
NBDirV-Type C-Type V-Cutoff C-Cutoff
V-Type, C-Type, V-Cutoff, and C-Cutoff as above.
Coulomb and Vanderwaals single term cutoffs
NBTermAtom-type1 Atom-type2 V-Type C-Type V-Cutoff C-Cutoff V-Scale C-Scale
V-Type, C-Type, V-Cutoff, C-Cutoff, V-Scale, and C-Scale as above.
Atomic single bond radius
AtRadAtom-type Radius
Effective charge (UFF)
EffChgCharge
GMP Electronegativity (UFF)
EleNegValue
Step down table
TableOriginal-atom-type Stepping-down-type(s).
Harmonic stretch I (Amber [1]): ForceC*(R-Req)2
HrmStr1Atom-type1 Atom-type2 ForceC Req
ForceC Force constant
Req Equilibrium bond length
Harmonic stretch II (Dreiding [4a]): ForceC*[R-(Ri+Rj-Delta)]2
HrmStr2 Atom-type1 Atom-type2 ForceC Delta
ForceC Force constant
Delta Delta
Ri and Rj are atomic bond radii specified with AtRad.
Harmonic stretch III (UFF [1a]): k*(R-Rij)2
Equilibrium bond length Rij = (1 - PropC*lnBO)*(Ri + Rj) + Ren
Force constant: k = 664.12*Zi*Zj/(Rij3)
Electronegativity correction: Ri*Rj*[Sqrt(Xi) - Sqrt(Xj)]2/(Xi*Ri + Xj*Rj)
HrmStr3Atom-type1 Atom-type2 BO PropC
BO Bond order (if <0, it is determined on-the-fly)
PropC Proportionality constant
Ri and Rj are atomic bond radii defined with AtRad. Xi and Xj are GMP electronegativity values defined with EleNeg. Zi and Zj are the effective atomic charges defined with EffChg.
Morse stretch I (Amber): DLim*(e-a(R-Req)-1)2 where a = Sqrt(ForceC/DLim)
MrsStr1 Atom-type1 Atom-type2 ForceC Req DLim
ForceC Force constant
Req Equilibrium bond length
DLim Dissociation limit
Morse stretch II (Dreiding [5a]): DLim*exp[-a(Ri+Rj-Delta)]-1)2 where a = Sqrt(ForceC/DLim)
MrsStr2 Atom-type1 Atom-type2 ForceC Delta DLim
ForceC Force constant
Delta Delta
DLim Dissociation limit
Ri and Rj are atomic bond radii defined with AtRad.
Morse stretch III (UFF [1b]): A1*A3*(exp[-a(R-Rij)]-1)2 where a = Sqrt(k/[BO*PropC])
Equilibrium bond length Rij = (1 - PropC*lnBO)*(Ri + Rj) + Ren
Force constant k = 664.12*Zi*Zj/Rij3
Electronegativity correction: Ren = Ri*Rj*(Sqrt(Xi) - Sqrt(Xj))2/(Xi*Ri + Xj*Rj)
MrsStr3Atom-type1 Atom-type2 BO PropC
BO Bond order (if <0, it is determined on-the-fly)
PropC Proportionality constant
Ri and Rj are atomic bond radii defined with AtRad. Xi and Xj are GMP electronegativity values defined with EleNeg. Zi and Zj are the effective atomic charges defined with EffChg.
Quartic stretch I (MMFF94 [2]):
(Req/2)*(R-ForceC)2*[1+CStr*(R-ForceC+(7/12)*CStr2*(R-ForceC)2]
QStr1Atom-type1 Atom-type2 ForceC Req CStr
ForceC Force constant (md-Angstrom-1)
Req Equilibrium bond length (Angstrom)
CStr Cubic stretch constant (Angstrom-1)
Atomic torsional barrier for the oxygen column (UFF [16])
UFFVOx Barrier
Atomic sp3 torsional barrier (UFF [16])
UFFVsp3 Barrier
Atomic sp2 torsional barrier (UFF [17])
UFFVsp2 Barrier
Harmonic bend (Amber [1]): ForceC*(T-θeq)2
HrmBnd1 Atom-type1 Atom-type2 Atom-type3 ForceC θeq
ForceC Force constant (in kcal/(mol*rad2)
θeq Equilibrium angle
Harmonic Bend (Dreiding [10a]): [ForceC/sin(θeq2)]*(cos(θ)-cos(θeq))2
HrmBnd2 Atom-type1 Atom-type2 Atom-type3 ForceC θeq
ForceC Force constant
θeq Equilibrium angle
Dreiding Linear Bend (Dreiding [10c]): AForceC*(1+cos(θ))
LinBnd1 Atom-type1 Atom-type2 Atom-type3 ForceC
ForceC Force constant
UFF 3-term bend (UFF [11]):
k*(C0 + C1*cos(θ))+C2*cos(2θ) where C2=1/(4 * sin(θeq2)),
C1 = -4*C2*cos(θeq) and C0=C2*(2*cos(θeq2)+1)
Force constant: k = 664.12*Zi*Zk*(3*Rij*Rjk*(1-cos(θeq2))-cos(θeq)*Rik2)/Rik5
UFFBnd3 Atom-type1 Atom-type2 Atom-type3 θeqBO12BO23PropC
θeq Equilibrium angle
BO12 Bond order for Atom-type1–Atom-type2 (when <0, it is determined on-the-fly)
BO23 Bond order for Atom-type2–Atom-type3 (when <0, it is determined on-the-fly)
PropC Proportionality constant
Ri, Rj and Rk are atomic bond radii defined with AtRad. Xi, Xj and Xk are GMP electronegativity defined with EleNeg. Zi, Zj and Zk are effective atomic charges defined with EffChg.
UFF 2-term bend (UFF [10]): [k/(Per2)]*[1-cos(Per*θ)]
Force constant: k = 664.12*Zi*Zk*(3*Rij*Rjk*(1-cos(Per2))-cos(Per)*Rik2)/Rik5
UFFBnd2 Atom-type1 Atom-type2 Atom-type3 Per BO12BO23PropC
Per Periodicity: 2 for linear, 3 for trigonal, 4 for square-planar.
BO12 Bond order for Atom-type1–Atom-type2 (when <0, it is determined on-the-fly)
BO23 Bond order for Atom-type2–Atom-type3 (when <0, it is determined on-the-fly)
PropC Proportionality constant
Ri, Rj and Rk are atomic bond radii defined with AtRad. Xi, Xj and Xk are GMP electronegativity defined with EleNeg. Zi, Zj and Zk are effective atomic charges defined with EffChg.
Zero bend term: used in rare cases where a bend is zero. This term is needed for the program not to protest about undefined angles.
ZeroBndAtom-type1 Atom-type2 Atom-type3
Cubic bend I (MMFF94 [3]): (ForceC/2)*(1+CBend*(θ-θeq))*(θ-θeq)2
CubBnd1Atom-type1 Atom-type2 Atom-type3 ForceC θeqCBend
ForceC Force constant (in md*Angstrom/rad2)
θeq Equilibrium angle
CBend 'Cubic Bend' constant (in deg-1)
MMFF94 Linear Bend (MMFF94 [4]): ForceC*(1+cos(θ))
LinBnd2Atom-type1 Atom-type2 Atom-type3 ForceC
ForceC Force constant (md)
Amber torsion (Amber [1]): Σi=1,4 (Magi*[1+cos(i*θ-I(i+4))])/NPaths
AmbTrsAtom-type1 A-type2 A-type3 A-type4 PO1 PO2 PO3 PO4 Mag1Mag2Mag3Mag4NPaths
PO1-PO4 Phase offsets
Mag1...Mag4V/2 magnitudes
NPaths Number of paths (if < 0, determined on-the-fly).
Dreiding torsion (Dreiding [13]): V*[1-cos(Period*(θ-PO))]/(2*NPaths)
DreiTrsAtom-type1 Atom-type2 Atom-type3 Atom-type4 V PO Period NPaths
V Barrier height V
PO Phase offset
Period Periodicity
NPaths Number of paths (if < 0, determined on-the-fly).
UFF torsion with constant barrier height (UFF [15]): [V/2]*[1-cos(Period*PO)*cos(V*θ)]/NPaths
UFFTorC Atom-type1 Atom-type2 Atom-type3 Atom-type4 Period PO V NPaths
Period Periodicity
PO Phase offset
V Barrier height V
NPaths Number of paths. When zero or less, determined on-the-fly.
UFF torsion with bond order based barrier height (UFF [17]):
[V/2]*[1-cos(Period*PO)* cos(Period*θ)]/NPaths where V = 5*Sqrt(Uj*Uk)*[1+4.18*Log(BO12)]
UFFTorB Atom-type1 Atom-type2 Atom-type3 Atom-type4 Period POBO12NPaths
Period Periodicity
PO Phase offset
BO12 Bond order for Atom-type1–Atom-type2 (when <0, it is determined on-the-fly)
NPaths Number of paths (when <0, it is determined on-the-fly)
Uj and Uk are atomic constants defined with UFFVsp2.
UFF torsion with atom type-based barrier height (UFF [16]):
[V/2]*[1-cos(Period*PO)* cos(Period*θ)]/NPaths where V=Sqrt(Vj*Vk)
UFFTor1Atom-type1 Atom-type2 Atom-type3 Atom-type4 Period PO NPaths
Period Periodicity
PO Phase offset
NPaths Number of paths. When zero or less, determined on-the-fly.
Vj and Vk are atomic constants defined with UFFVsp3.
UFF torsion with atom type based barrier height (UFF [16]) (differs from UFFTor1 in that the atomic parameter that is used): [V/2]*[1-cos(Period*PO)*cos(Period*θ)]/NPAths where V=Sqrt(Vj*Vk)
UFFTor2 Atom-type1 Atom-type2 Atom-type3 Atom-type4 Period PO NPaths
Period Periodicity
PO Phase offset
NPaths Number of paths. When zero or less, determined on-the-fly.
Vj and Vk are atomic constants from UFFVOx.
Dreiding special torsion for compatibility with Gaussian 98 code. During processing, it is replaced with DreiTRS, with the following parameters:
If there are three atoms bonded to the third center and the fourth center is H, it is removed.
If there are three atoms bonded to the third center, and at least one of them is H, but the fourth center is not H, then these values are used: V=4.0, PO=0.0, Period=3.0, and NPaths=-1.0.
Otherwise, these values are used: V=1.0, PO=0.0, Period=6.0, and NPaths=-1.0.
OldTor Atom-type1 Atom-type2 Atom-type3 Atom-type4
Improper torsion (Amber [1]): Mag*[1+cos(Period*(θ-PO))]
ImpTrs Atom-type1 Atom-type2 Atom-type3 Atom-type4 Mag PO Period
Mag V/2 Magnitude
PO Phase offset
Period Periodicity
Three term Wilson angle (Dreiding [28c], UFF [19]): ForceC*(C1 + C2*cos(θ) + C3*cos(2θ)) averaged over all three Wilson angles θ.
WilsonAtom-type1 Atom-type2 Atom-type3 Atom-type4 ForceC C1 C2 C3
ForceC Force constant
C1, C2, C3 Coefficients
Harmonic Wilson angle (MMFF94 [6]): (ForceC/2)*(θ2) summed over all three Wilson angles θ.
HrmWilAtom-type1 Atom-type2 Atom-type3 Atom-type4 ForceC
ForceC Force constant
Stretch-bend I (MMFF94 [5]): (ForceC1*(R12-Req12)+ForceC2*(R32-Req23))*(θ-θeq)
StrBnd1Atom-type1 Atom-type2 Atom-type3 ForceC1 ForceC2 Req12Req23 θeq
ForceC1, ForceC2 Force constants (in md/rad)
Req12, Req23Equilibrium bond lengths
θeq Equilibrium angle
USING SUBSTRUCTURES
Substructures may be used to define different parameter values for a function for distinct ranges of some geometrical characteristic. Substructure numbers are appended to the function name, separated by a hyphen (e.g., HrmStr-1, HrmStr-2 and so on).
The following substructures apply to functions related to bond stretches:
-1 Single bond: 0.00 ≤ bond order < 1.50
-2 Double bond: 1.50 ≤bond order < 2.50
-3 Triple bond: bond order ≥ 2.50
The following substructures apply to functions for bond angles (values in degrees):
First substructure:
-1 0 ≤ θ ≤ 45
-2 45 < θ ≤ 135
-3 135 < θ ≤ 180
Second substructure:
-i-n Number of atoms bonded to the central one.
For dihedral angles, one or two substructures may be used (e.g., AmbTrs-1-2). Use a zero for the first substructure to specify only the second substructure.
First substructure:
-0 Skip this substructure (substructure 'wildcard')
-1 Single central bond: 0.00 ≤ bond order < 1.50
-2 Double central bond: 1.50 ≤ bond order < 2.50
-3 Triple central bond: bond order ≥ 2.50
Second substructure:
-i-1 Resonance central bond (1.30 ≤ bond order ≤ 1.70)
-i-2 Amide central bond (priority over resonance)
-i-3 None of the above
Here is some simple MM force field definition input:
Next:The Integrals-With-Labels Library Up:The Checkpoint File Library Previous:InitializationContentsFunctions for reading information from the checkpoint file
char *file30_rd_corr_lab()Reads in a label from file30 which describes thewavefunction used to get the correlated energy which is stored infile30 (see
| Arguments: | takes no arguments. |
| Returns: | a string, like 'CISD', or 'MCSCF' orsome other wavefunction designation. |
char *file30_rd_label()
Reads the main file30 label.
| Arguments: | takes no arguments. |
| Returns: | calculation label. |
char *file30_rd_sym_label()
Reads the label for the point group.
| Arguments: | takes no arguments. |
| Returns: | point group label. |
Read in the symmetry labels for all irreps in thepoint group in which the molecule is considered.
| Arguments: | takes no arguments. |
| Returns: | an array of labels (strings) which denotethe irreps for the point group in which the molecule is considered,_regardless_ of whether there exist any symmetry orbitals whichtransform as that irrep. |
char **file30_rd_hfsym_labs()
Read in the symmetry labels _only_ for those irrepswhich have basis functions.
| Arguments: | takes no arguments. |
| Returns: | an array of labels (strings) which denotethe irreps which have basis functions (in Cotton ordering). For DZ orSTO-3G water, for example, in symmetry, this would be an array ofthree labels: 'A1', 'B1', and 'B2'. |
Reads in the dimensionality (up to a sign) of ALPHA and BETA vectors of two-electron coupling coefficients for open shells. (see file30_rd_ccvecs())Note : iopen = MM * (MM + 1), where MM is the total number ofirreps containing singly occupied orbitals.
| Arguments: | takes no arguments. |
| Returns: | the +/- dimensionality of ALPHA and BETA vectors of coupling coefficients for open shells. |
int file30_rd_max_am()
Reads in the maximum orbital quantum number of AOs in the basis.
| Arguments: | takes no arguments. |
| Returns: | the maximum orbital quantum number of AOs in the basis. |
int file30_rd_mxcoef()
Reads the value of the constant mxcoef.
| Arguments: | takes no arguments. |
| Returns: | the sum of the squares of the number of symmetryorbitals for each irrep. This gives the number of elements in thenon-zero symmetry blocks of the SCF eigenvector. For STO-3G watermxcoef. |
int file30_rd_nao()
Reads in the total number of atomic orbitals (read: Cartesian Gaussian functions).
| Arguments: | takes no arguments. |
| Returns: | total number of atomic orbitals. |
int file30_rd_natom()
Reads in the total number of atoms.
| Arguments: | takes no arguments. |
| Returns: | total number of atoms. |
int file30_rd_ncalcs()
Reads in the total number of calculations (always 1).
| Arguments: | takes no arguments. |
| Returns: | total number of calculations in file30. |
 int file30_rd_nirreps()
int file30_rd_nirreps()Reads in the total number of irreducible representationsin the point group in which the molecule is being considered.
| Arguments: | takes no arguments. |
| Returns: | total number of irreducible representations. |
int file30_rd_nmo()
Reads in the total number of molecular orbitals (may be differentfrom the number of basis functions).
| Arguments: | takes no arguments. |
| Returns: | total number of molecular orbitals. |
int file30_rd_nprim()
Reads in the total number of primitive Gaussian functions (only primitives of _symmetry independent_ atoms are counted!).
| Arguments: | takes no arguments. |
| Returns: | total number of primitive Gaussian functions. |
int file30_rd_nshell()
Reads in the total number of shells. For example, DZP basis set for carbon atom (contraction scheme ) has a total of 15 basis functions, 15 primitives, and 7 shells. Shells of _all_ atoms are counted(not only of the symmetry independent; compare file30_rd_nprim).
| Arguments: | takes no arguments. |
| Returns: | total number of shells. |
int file30_rd_nso()
Reads in the total number of symmetry-adapted basis functions (read:Cartesian or Spherical Harmonic Gaussians).
| Arguments: | takes no arguments. |
| Returns: | total number of SOs. |
int file30_rd_nsymhf()
Reads in the total number of irrepsin the point group in which the molecule is being considered whichhave non-zero number of basis functions. For STO-3G or DZ water, forexample, this is three, even though nirreps is 4 (compareint file30_rd_nirreps()).
| Arguments: | takes no arguments. |
| Returns: | total number of irreducible representationswith a non-zero number of basis functions. |
int file30_rd_num_unique_atom()
Reads in the number of symmetry unique atoms.
| Arguments: | takes no arguments. |
| Returns: | number of symmetry unique atoms. |
int file30_rd_num_unique_shell()
Reads in the number of symmetry unique shells.
| Arguments: | takes no arguments. |
| Returns: | number of symmetry unique shells. |
int file30_rd_phase_check()
Reads the phase flag???
| Arguments: | takes no arguments. |
| Returns: | flag. |
Reads the reference type from the flag in file30.0 = RHF, 1 = UHF, 2 = ROHF, 3 = TCSCF.
| Arguments: | takes no arguments. |
| Returns: | flag indicating the reference. |
Reads the rigid rotor type the molecule represents.0 = asymmetric, 1 = symmetric, 2 = spherical, 3 = linear, 6 = atom.
| Arguments: | takes no arguments. |
| Returns: | rigid rotor type. |
Reads in the the mapping array from the angmom-orderedto the canonical (in the order of appearance) list of shells.
| Arguments: | takes no arguments. |
| Returns: | an array nshell long that maps shells from the angmom-orderedto the canonical (in the order of appearance) order. |
Reads in symmetry positions of atoms.Allowed values are as follows:
- 1 - atom in a general position
- 2 - atom on the c2z axis
- 4 - atom on the c2y axis
- 8 - atom on the c2x axis
- 16 - atom in the inversion center
- 32 - atom in the sigma_xy plane
- 64 - atom in the sigma_xz plane
- 128 - atom in the sigma_yz plane
| Arguments: | takes no arguments. |
| Returns: | an array of symmetry positions of atoms. |
int *file30_rd_clsdpi()
Reads in an array which has an element for each irrep of thepoint group of the molecule (n.b. not just the oneswith a non-zero number of basis functions). Each elementcontains the number of doubly occupied MOs for that irrep.
| Arguments: | takes no arguments. |
| Returns: | the number of doubly occupied MOs per irrep. |
int *file30_rd_openpi()
Reads in an array which has an element for each irrep of thepoint group of the molecule (n.b. not just the oneswith a non-zero number of basis functions). Each elementcontains the number of singly occupied MOs for that irrep.
| Arguments: | takes no arguments. |
| Returns: | the number of singly occupied MOs per irrep. |
Read Checkpoint File Gaussian Software
int *file30_rd_orbspi()Reads in the number of MOs in each irrep.
| Arguments: | takes no arguments. |
| Returns: | the number of MOs in each irrep. |
int *file30_rd_shells_per_am()
Reads in the number of shells in each angmom block.
| Arguments: | takes no arguments. |
| Returns: | the number of shells in each angmom block. |
file30_rd_sloc()
Read in an array of pointers to the first AOfrom each shell.
| Arguments: | takes no arguments. |
| Returns: | Read in an array nshell long of pointers tothe first AO from each shell. |
file30_rd_sloc_new()
Read in an array of pointers to the first basisfunction (not AO as file30_rd_sloc does)from each shell.
| Arguments: | takes no arguments. |
| Returns: | an array nshell long of pointers tothe first basis function from each shell. |
int *file30_rd_snuc()
Reads in an array of pointers to the nuclei on which shells are centered.
| Arguments: | takes no arguments. |
| Returns: | an array nshell long of pointers to the nuclei on which shellsare centered. |
Reads in array of the numbers of the primitiveGaussians in the shells.
| Arguments: | takes no arguments. |
| Returns: | an array nshell long of the numbers of the primitive Gaussians in shells. |
int *file30_rd_sprim()
Reads in pointers to the first primitivefrom each shell.
| Arguments: | takes no arguments. |
| Returns: | an array nshell long of pointers to the first primitive from each shells. |
file30_rd_sopi()
Read in the number of symmetry-adapted basis functions in each symmetry block.
| Arguments: | takes no arguments. |
| Returns: | an array nirreps long of the numbers ofsymmetry orbitals in symmetry blocks. |
int *file30_rd_stype()
Reads in angular momentum numbers ofthe shells.
| Arguments: | takes no arguments. |
| Returns: | Returns an array nshell long ofthe angular momentum numbers of the shells. |
int *file30_rd_symoper()
Read in the mapping array between 'canonical' orderingof the symmetry operations of the point group and theone defined in symmetry.h.
| Arguments: | takes no arguments. |
| Returns: | a mapping array nirrep long |
Read in the mapping array from the symmetry-unique atom list to the full atom list.
| Arguments: | takes no arguments. |
| Returns: | a mapping array num_unique_atom long |
Read in the mapping array from the symmetry-unique shell listto the full shell list.
| Arguments: | takes no arguments. |
| Returns: | a mapping array num_unique_shell long |
Reads the transformation properties of the nucleiunder the operations allowed for the particular symmetry point groupin which the molecule is considered.
| Arguments: | takes no arguments. |
| Returns: | a matrix of integers. Each row correspondsto a particular symmetry operation, while each column corresponds toa particular atom. The value of ict[2][1], then, should be interpretedin the following manner: application of the third symmetry operation of the relavant point group, the second atom is placed in the locationoriginally occupied by the atom number ict[2][1]. |
int **file30_rd_shell_transm()
Reads in the transformation matrix for the shells. Each row of the matrix is the orbit of the shell under symmetry operations of the point group.
| Arguments: | takes no arguments. |
| Returns: | a matrix of nshell*nirreps integers. |
Reads in the correlation energy stored in file30. To get someinformation (a label) on the type of correlated wavefunctionused to get this energy, see file30_rd_corr_lab().
| Arguments: | takes no arguments. |
| Returns: | the correlation energy. |
double file30_rd_enuc()
Reads in the nuclear repulsion energy
| Arguments: | takes no arguments. |
| Returns: | the nuclear repulsion energy. |
double file30_rd_eref()
Reads in the reference energy (may be different from HF energy).
| Arguments: | takes no arguments. |
| Returns: | the reference energy. |
double file30_rd_escf()
Reads in the SCF HF energy.
| Arguments: | takes no arguments. |
| Returns: | the SCF HF energy. |
double *file30_rd_alpha_evals()
double *file30_rd_beta_evals()
Reads in the (spin-restricted HF, UHF, and UHF) eigenvalues:the orbital energies.
| Arguments: | take no arguments. |
| Returns: | an array of _all_ of the SCF eigenvalues,ordered by irrep, and by increasing energy within each irrep.(i.e. for STO-3G water, the four eigenvalues all come first, andthose four are ordered from lowest energy to highest energy,followed by the single eigenvalue, etc. -- Pitzer ordering) |
double *file30_rd_exps()
Reads in the exponents of the primitive Gaussian functions.
| Arguments: | takes no arguments. |
| Returns: | an array of doubles. |
Read Checkpoint File Gaussian Free
double *file30_rd_zvals()Reads in nuclear charges.
| Arguments: | takes no arguments. |
| Returns: | an array natom long of nuclear charges (as doubles). |
double **file30_rd_alpha_blk_scf(int irrep)
double **file30_rd_beta_blk_scf(int irrep)
Reads in a symmetry block of the (RHF, UHF, UHF) eigenvector.
| Arguments: | int irrep, designates the desired symmetry block |
| Returns: | a square matrix has orbspi[irrep]rows. The eigenvectors are stored with the column index denoting MOs and the row index denoting SOs: this means that scf_vector[i][j] is the contribution of the th SO to the th MO. |

double **file30_rd_ccvecs()
Reads in a matrix rows of which are ALPHA (ccvecs[0]) and BETA (ccvecs[1]) matrices of couplingcoefficients for open shells stored in lower triangular form.Coupling coefficients are defined NOT as in C.C.J.Roothaan Rev. Mod. Phys. 32, 179 (1960) as it is stated in themanual pages for CSCF, but according to Pitzer (no reference yet)and are **different** from those in Yamaguchi, Osamura, Goddard, andSchaefer's book 'Analytic Derivative Methods in Ab Initio MolecularElectronic Structure Theory'.
The relationship between the Pitzer's and Yamaguchi's conventions is as follows : ALPHA = 1-2*a , BETA = 1+4*b , where a and b are alpha's and beta's for open shells defined on pp. 69-70 of Dr. Yamaguchi's book.
| Arguments: | takes no arguments. |
| Returns: | double **ccvecs, a matrix 2 by abs(iopen) rows of which are couplingcoefficient matrices for open-shells in packed form.For definition of iopen see file30_rd_iopen(). |
file30_rd_contr_full()
Reads in the normalized contraction coefficients.
| Arguments: | takes no arguments. |
| Returns: | a matrix MAXANGMOM (a constant defined in file30_params.h)by the total number of primitives nprim;each primitive Gaussian contributes to only one shell (and onebasis function, of course), so most of these values are zero. |
double **file30_rd_geom()
Reads in the cartesian geometry.
| Arguments: | takes no arguments. |
| Returns: | The cartesian geometry is returned as a matrixof doubles. The row index is the atomic index, and the column is thecartesian direction index (x=0, y=1, z=2). Therefore, geom[2][0]would be the x-coordinate of the third atom. |
file30_rd_lagr()
file30_rd_alpha_lagr()
file30_rd_beta_lagr()
Reads in an (RHF, UHF, UHF) Lagrangian matrix in MO basis.
| Arguments: | takes no arguments. |
| Returns: | a matrix nmo by nmo. |
double **file30_rd_scf()
double **file30_rd_alpha_scf()
double **file30_rd_beta_scf()
Reads in the (RHF, UHF, UHF) eigenvector.
| Arguments: | takes no arguments. |
| Returns: | a square matrix of dimensions nmoby nmo (see: file30_rd_nmo()).The symmetry blocks of the SCF vector appearon the diagonal of this matrix. |
file30_rd_schwartz()
Reads in the table of maxima of Schwartz integrals (ij|ij)for each shell doublet.
| Arguments: | takes no arguments. |
| Returns: | NULL if no table is present in the checkpoint file,a matrix nshell by nshell otherwise. |
file30_rd_usotao_new()
Reads in an AO to SO transformation matrix.
| Arguments: | takes no arguments. |
| Returns: | a nso by nao matrix of doubles. |
file30_rd_usotbf()
Reads in a basis function to SO transformation matrix.
| Arguments: | takes no arguments. |
| Returns: | a nso by nso matrix of doubles. |
file30_rd_zmat()
Reads in the z-matrix
| Arguments: | takes no arguments. |
| Returns: | struct*z_entry natom long. |
Read Checkpoint File Gaussian Pdf
Next:The Integrals-With-Labels Library Up: